FUNDAMENTOS-DT

 O que é desenho técnico

 

Quando alguém quer transmitir um recado, pode utilizar a fala ou passar seus pensamentos para o papel na forma de palavras escritas. Quem lê a mensagem fica conhecendo os pensamentos de quem a escreveu. Quando alguém desenha, acontece o mesmo: passa seus pensamentos para o papel na forma de desenho. A escrita, a fala e o desenho representam idéias e pensamentos. A representação que vai interessar neste curso é o desenho.

 

Desde épocas muito antigas, o desenho é uma forma importante de comunicação. E essa representação gráfica trouxe grandes contribuições para a compreensão da História, porque, por meio dos desenhos feitos pelos povos antigos, podemos conhecer as técnicas utilizadas por eles, seus hábitos e até suas idéias.

 

 

As atuais técnicas de representação foram criadas com o passar do tempo, à medida que o homem foi desenvolvendo seu modo de vida, sua cultura. Veja algumas formas de representação da figura humana, criadas em diferentes épocas históricas.

 

 

Desenho das cavernas de Skavberg (Noruega) do período mesolítico (6000 - 4500 a.C.).

Representação esquemática da figura humana.

 

Representação egípcia do túmulo do escriba Nakht, século XIV a.C.

Representação plana que destaca o contorno da figura humana.

 

Nu, desenhado por Miguel Ângelo Buonarroti (1475-1564).

Aqui, a representação do corpo humano transmite a idéia de volume.

 

Esses exemplos de representação gráfica são considerados desenhos artísticos. Embora não seja artístico, o desenho técnico também é uma forma de representação gráfica, usada, entre outras finalidades, para ilustrar instrumentos de trabalho, como máquinas, peças e ferramentas.

 

E esse tipo de desenho também sofreu modificações, com o passar do tempo.

 

Quais as diferenças entre o desenho técnico e o desenho artístico?

 

O desenho técnico é um tipo de representação gráfica utilizado por profissionais de uma mesma área, como, por exemplo, na mecânica, na marcenaria, na eletricidade.

 

Maiores detalhes sobre o desenho técnico você aprenderá no decorrer deste curso. Por enquanto, é importante que você saiba as diferenças que existem entre o desenho técnico e o desenho artístico. Para isso, é necessário conhecer bem as características de cada um. Observe os desenhos abaixo:

 

Cabeça de Criança, de Rosalba Carreira (1675-1757).

Paloma, de Pablo Picasso (1881-1973).

 

Estes são exemplos de desenhos artísticos. Os artistas transmitiram suas idéias e seus sentimentos de maneira pessoal. Um artista não tem o compromisso de retratar fielmente a realidade. O desenho artístico reflete o gosto e a sensibilidade do artista que o criou.

 

Já o desenho técnico, ao contrário do artístico, deve transmitir com exatidão todas as características do objeto que representa. Para conseguir isso, o desenhista deve seguir regras estabelecidas previamente, chamadas de normas técnicas.

 

Assim, todos os elementos do desenho técnico obedecem a normas técnicas, ou seja, são normalizados. Cada área ocupacional tem seu próprio desenho técnico, de acordo com normas específicas. Observe alguns exemplos.

 

 

Nesses desenhos, as representações foram feitas por meio de traços, símbolos, números e indicações escritas, de acordo com normas técnicas.

 

No Brasil, a entidade responsável pelas normas técnicas é a ABNT - Associação Brasileira de Normas Técnicas. Neste curso você vai conhecer a aplicação das principais normas técnicas referentes ao desenho técnico mecânico, de acordo com a ABNT.

 

Como é elaborado um desenho técnico

 

Às vezes, a elaboração do desenho técnico mecânico envolve o trabalho de vários profissionais. O profissional que planeja a peça é o engenheiro ou o projetista. Primeiro ele imagina como a peça deve ser.

 

Depois representa suas idéias por meio de um esboço, isto é, um desenho técnico à mão livre. O esboço serve de base para a elaboração do desenho preliminar. O desenho preliminar corresponde a uma etapa intermediária do processo de elaboração do projeto, que ainda pode sofrer alterações.

 

Depois de aprovado, o desenho que corresponde à solução final do projeto será executado pelo desenhista técnico. O desenho técnico definitivo, também chamado de desenho para execução, contém todos os elementos necessários à sua compreensão.

 

O desenho para execução, que tanto pode ser feito na prancheta como no computador, deve atender rigorosamente a todas as normas técnicas que dispõem sobre o assunto.

 

O desenho técnico mecânico chega pronto às mãos do profissional que vai executar a peça. Esse profissional deve ler e interpretar o desenho técnico para que possa executar a peça. Quando o profissional consegue ler e interpretar corretamente o desenho técnico, ele é capaz de imaginar exatamente como será a peça, antes mesmo de executá-la. Para tanto, é necessário conhecer as normas técnicas em que o desenho se baseia e os princípios de representação da geometria descritiva.

 

 

Geometria descritiva: a base do desenho técnico

 

O desenho técnico, tal como nós o entendemos hoje, foi desenvolvido graças ao matemático francês Gaspar Monge (1746-1818). Os métodos de representação gráfica que existiam até aquela época não possibilitavam transmitir a idéia dos objetos de forma completa, correta e precisa.

 

Monge criou um método que permite representar, com precisão, os objetos que têm três dimensões (comprimento, largura e altura) em superfícies planas, como, por exemplo, uma folha de papel, que tem apenas duas dimensões (comprimento e largura).

 

Esse método, que passou a ser conhecido como método mongeano, é usado na geometria descritiva. E os princípios da geometria descritiva constituem a base do desenho técnico. Veja:

 

 

À primeira vista, pode parecer complicado. Mas, não se preocupe. Acompanhando este curso, você será capaz de entender a aplicação da geometria descritiva no desenho técnico. Basta aprender ou recordar algumas noções básicas de geometria, que serão apresentadas na próxima aula.

 

HISTÓRICO

 

Figuras geométricas

 

            Se olhar ao seu redor, você verá que os objetos têm forma, tamanho e outras características próprias. As figuras geométricas foram criadas a partir da observação   das formas existentes na natureza e dos objetos produzidos pelo homem.

 

 

   Nesta aula você vai conhecer ou recordar os diversos tipos de figuras geométricas. Todos os objetos, mesmo os mais complexos, podem ser associados a um            conjunto de figuras geométricas.

 

   Você terá mais facilidade para ler e interpretar desenhos técnicos mecânicos se for capaz de relacionar objetos e peças da área da Mecânica às figuras           geométricas.

 

Figuras geométricas elementares

 

                Ponto

 

      Pressione seu lápis contra uma folha de papel. Observe a marca deixada pelo lápis: ela representa um ponto. Olhe para o céu, numa noite sem nuvens: cada estrela      pode ser associada a um ponto.

 

      O ponto é a figura geométrica mais simples. Não tem dimensão, isto é, não tem comprimento, nem largura, nem altura.

 

      No desenho, o ponto é determinado pelo cruzamento de duas linhas. Para identificá-lo, usamos letras maiúsculas do alfabeto latino, como mostram os exemplos:

 

 

                Linha

 

      Podemos ter uma idéia do que é linha, observando os fios que unem os postes de eletricidade ou o traço que resulta do movimento da ponta de um lápis sobre uma          folha de papel.

 

      A linha tem uma única dimensão: o comprimento.

 

Você pode imaginar a linha como um conjunto infinito de pontos dispostos sucessivamente. O deslocamento de um ponto também gera uma linha.

 

                Linha reta ou reta

 

Para se ter a idéia de linha reta, observe um fio bem esticado. A reta é ilimitada, isto é, não tem início nem fim. As retas são identificadas por letras minúsculas do alfabeto latino. Veja a representação da uma reta r:

 

 

                Semi-reta

 

            Tomando um ponto qualquer de uma reta, dividimos a reta em duas partes, chamadas semi-retas. A semi-reta sempre tem um ponto de origem, mas não tem fim.

 

 

                Segmento de reta

 

Tomando dois pontos distintos sobre uma reta, obtemos um pedaço limitado de reta. A esse pedaço de reta, limitado por dois pontos, chamamos segmento de reta.     

Os pontos que limitam o segmento de reta são chamados de extremidades.

 

               No exemplo a seguir temos o segmento de reta CD, que é representado da seguinte maneira: CD.

 

                                                                                              Os pontos C e D (extremidades) determinam o segmento de reta CD.

 

 

                        Plano

 

Podemos ter uma idéia do que é o plano observando uma parede ou o tampo de uma mesa.

 

Você pode imaginar o plano como sendo formado por um conjunto de retas dispostas sucessivamente numa mesma direção ou como o resultado do deslocamento de uma reta numa mesma direção. O plano é ilimitado, isto é, não tem começo nem fim. Apesar disso, no desenho, costuma-se representá-lo delimitado por linhas fechadas:

 

 

            Para identificar o plano usamos letras gregas. É o caso das letras: α (alfa), β (beta) e y (gama), que você pode ver nos planos representados na figura acima.

 

   O plano tem duas dimensões, normalmente chamadas comprimento e largura. Se tomamos uma reta qualquer de um plano, dividimos o plano em duas partes,             chamadas semi-planos.

 

Posições da reta e do plano no espaço

 

A geometria, ramo da Matemática que estuda as figuras geométricas, preocupa-se também com a posição que os objetos ocupam no espaço.

 

A reta e o plano podem estar em posição vertical, horizontal ou inclinada.

 

Um tronco boiando sobre a superfície de um lago nos dá a idéia de uma reta horizontal. O pedreiro usa o prumo para verificar a verticalidade das paredes.

 

O fio do prumo nos dá a idéia de reta vertical.

 

Um plano é vertical quando tem pelo menos uma reta vertical; é horizontal quando todas as suas retas são horizontais. Quando não é horizontal nem vertical, o plano é inclinado. Veja as posições da reta e do plano.

 

 

Figuras geométricas planas

 

Uma figura qualquer é plana quando todos os seus pontos situam-se no mesmo plano.

 

A seguir você vai recordar as principais figuras planas. Algumas delas você terá de identificar pelo nome, pois são formas que você encontrará com muita freqüência em desenhos mecânicos.

 

Observe a representação de algumas figuras planas de grande interesse para nosso estudo:

 

As figuras planas com três ou mais lados são chamadas polígonos.

 

Sólidos geométricos

 

Você já sabe que todos os pontos de uma figura plana localizam-se no mesmo plano. Quando uma figura geométrica tem pontos situados em diferentes planos, temos um sólido geométrico.

 

Analisando a ilustração abaixo, você entenderá bem a diferença entre uma figura plana e um sólido geométrico.

 

 

Os sólidos geométricos têm três dimensões: comprimento, largura e altura.

 

Embora existam infinitos sólidos geométricos, apenas alguns, que apresentam determinadas propriedades, são estudados pela geometria. Os sólidos que você estudará neste curso têm relação com as figuras geométricas planas mostradas anteriormente.

 

Os sólidos geométricos são separados do resto do espaço por superfícies que os limitam. E essas superfícies podem ser planas ou curvas.

 

Dentre os sólidos geométricos limitados por superfícies planas, estudaremos os prismas, o cubo e as pirâmides. Dentre os sólidos geométricos limitados por superfícies curvas, estudaremos o cilindro, o cone e a esfera, que são também chamados de sólidos de revolução.

 

É muito importante que você conheça bem os principais sólidos geométricos porque, por mais complicada que seja, a forma de uma peça sempre vai ser analisada como o resultado da combinação de sólidos geométricos ou de suas partes.

 

Prismas

 

   O prisma é um sólido geométrico limitado por polígonos. Você pode imaginá-lo como uma pilha de polígonos iguais muito próximos uns dos outros, como mostra a   ilustração:

 

 

                 O prisma pode também ser imaginado como o resultado do deslocamento de um polígono. Ele é constituído de vários elementos. Para quem lida com desenho técnico é muito importante conhecê-los bem. Veja quais são eles nesta ilustração:

 

 

 

 

Note que a base desse prisma tem a forma de um retângulo. Por isso ele recebe o nome de prisma retangular.

 

Dependendo do polígono que forma sua base, o prisma recebe uma denominação específica. Por exemplo: o prisma que tem como base o triângulo é chamado prisma triangular.

 

Quando todas as faces do sólido geométrico são formadas por figuras geométricas iguais, temos um sólido geométrico regular.

 

O prisma que apresenta as seis faces formadas por quadrados iguais recebe o nome de cubo.

 

Pirâmides

 

            A pirâmide é outro sólido geométrico limitado por polígonos. Você pode imaginá-la como um conjunto de polígonos semelhantes, dispostos uns sobre os outros, que diminuem de tamanho indefinidamente.

           

            Outra maneira de imaginar a formação de uma pirâmide consiste em ligar todos os pontos de um polígono qualquer a um ponto P do espaço.

 

            É importante O nome da pirâmide depende do polígono que forma sua base. Na figura ao lado, temos uma pirâmide quadrangular, pois sua base é um quadrado.

 

   O número de faces da pirâmide é sempre igual ao número de lados do polígono que forma sua base mais um. Cada lado do polígono da base é também uma aresta da pirâmide que você conheça também os elementos da pirâmide:

 

 

 

O número de arestas é sempre igual ao número de lados do polígono da base vezes dois. O número de vértices é igual ao número de lados do polígono da base mais um. Os vértices são formados pelo encontro de três ou mais arestas. O vértice principal é o ponto de encontro das arestas laterais.

 

 

Sólidos de revolução

 

Alguns sólidos geométricos, chamados sólidos de revolução, podem ser formados pela rotação de figuras planas em torno de um eixo.

 

Rotação significa ação de rodar, dar uma volta completa. A figura plana que dá origem ao sólido de revolução chama-se figura geradora. A linha que gira ao redor   do eixo formando a superfície de revolução é chamada linha geratriz.

 

      O cilindro, o cone e a esfera são os principais sólidos de revolução.

 

Cilindro

 

O cilindro é um sólido geométrico, limitado lateralmente por uma superfície curva. Você pode imaginar o cilindro como resultado da rotação de um retângulo ou de um quadrado em torno de um eixo que passa por um de seus lados. Veja a figura ao lado.

 

No desenho, está representado apenas o contorno da superfície cilíndrica. A figura plana que forma as bases do cilindro é o círculo. Note que o encontro de cada base com a superfície cilíndrica forma as arestas.

 

 

Cone

 

   O cone também é um sólido geométrico limitado lateralmente por uma superfície curva. A formação do cone pode ser imaginada pela rotação de um triângulo           retângulo em torno de um eixo que passa por um dos seus catetos.

 

      A figura plana que forma a base do cone é o círculo. O vértice é o ponto de encontro de todos os segmentos que partem do círculo. No desenho está representado           apenas o contorno da superfície cônica. O encontro da superfície cônica com a base dá origem a uma aresta.

 

 

 

                               Dica - Triângulo retângulo é o triângulo que apresenta um ângulo interno de 900.

 

Esfera

 

A esfera também é um sólido geométrico limitado por uma superfície curva chamada superfície esférica. Podemos imaginar a formação da esfera a partir da rotação de um semicírculo em torno de um eixo, que passa pelo seu diâmetro.

 

Veja os elementos da esfera na figura abaixo.

 

 

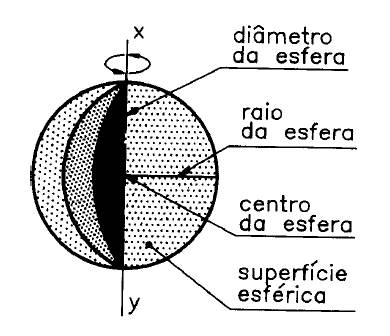
O raio da esfera é o segmento de reta que une o centro da esfera a qualquer um de seus pontos. Diâmetro da esfera é o segmento de reta que passa pelo centro da esfera unindo dois de seus pontos.

 

Sólidos geométricos truncados

 

                 Quando um sólido geométrico é cortado por um plano, resultam novas figuras geométricas: os sólidos geométricos truncados. Veja alguns exemplos de sólidos           truncados, com seus respectivos nomes:

 

 

Sólidos geométricos vazados

 

   Os sólidos geométricos que apresentam partes ocas são chamados sólidos geométricos vazados. As partes extraídas dos sólidos geométricos, resultando na parte            oca, em geral também correspondem aos sólidos geométricos que você já conhece.

  

   Observe a figura, notando que, para obter o cilindro vazado com um furo quadrado, foi necessário extrair um prisma quadrangular do cilindro original.

 

 

 

 

           

Comparando sólidos geométricos e objetos da área da Mecânica

 

         As relações entre as formas geométricas e as formas de alguns objetos da área da Mecânica são evidentes e imediatas. Você pode comprovar esta afirmação           analisando os exemplos a seguir.

 

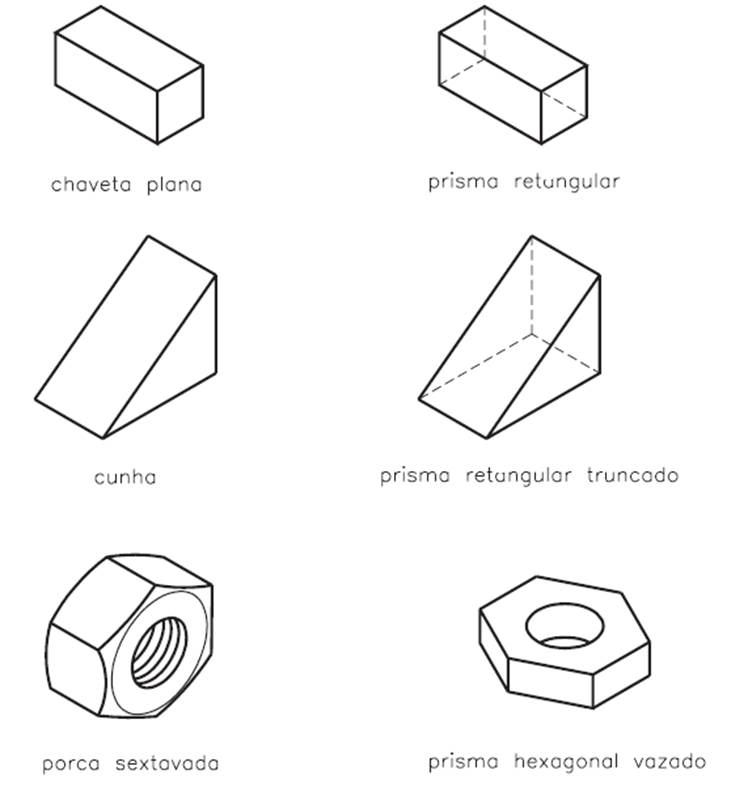
Há casos em que os objetos têm formas compostas ou apresentam vários elementos. Nesses casos, para entender melhor como esses objetos se relacionam com os sólidos geométricos, é necessário decompô-los em partes mais simples.

 

Analise cuidadosamente os próximos exemplos. Assim, você aprenderá a enxergar formas geométricas nos mais variados objetos.

 

Examine este rebite de cabeça redonda:

 

 

            Imaginando o rebite decomposto em partes mais simples, você verá que ele é formado por um cilindro e uma calota esférica (esfera truncada).

 

 

            Existe outro modo de relacionar peças e objetos com sólidos geométricos.

 

            Observe, na ilustração abaixo, como a retirada de formas geométricas de um modelo simples (bloco prismático) da origem a outra forma mais complexa.

 

 

            Nos processos industriais o prisma retangular é o ponto de partida para a obtenção de um grande número de objetos e peças.

Observe a figura abaixo. Trata-se de um prisma retangular com uma parte rebaixada que corresponde ao modelo de plástico nº 1. Veja como foi obtido o rebaixo:

 

                        A próxima ilustração mostra o desenho de um modelo que também deriva de um prisma retangular.

 

Elaborado por: Prof. Edilson José Barbosa 

Cefet/MG Campus  VII  - Timóteo

DMQ - TM - Departamento de Metalurgia e  Química

Curso : Engenharia  Metalúrgica